XV. Plus de structures de contrôle (obscures)▲
Dans le chapitre 2, un certain nombre de structures de contrôle ont été introduites, comme while, for, et break. Pour garder les choses simples, j'en ai laissé d'autres de côté, qui, d'après mon expérience, sont beaucoup moins utiles. Cet appendice décrit rapidement ces structures de contrôles manquantes.
Pour commencer, il y a do. do fonctionne comme while, mais au lieu d'exécuter zéro ou plusieurs fois, il l'exécute une ou plusieurs fois. Une boucle do ressemble à ceci :
do {
var reponse = prompt("Dites 'meuh'.", "");
print("Vous avez dit '", reponse , "'.");
} while (reponse != "meuh");Pour bien montrer que la condition est seulement testée après une première exécution, on l'écrit à la fin du corps de la boucle.
Ensuite, il y a continue. Celui-là est très lié à break et peut être utilisé aux mêmes endroits. Alors que le break saute en dehors de la boucle et fait continuer le programme après la boucle, continue saute à l'itération suivante de la boucle.
for (var i = 0; i < 10; i++) {
if (i % 3 != 0)
continue;
print(i, " est divisible par trois.");
}Un effet similaire peut en général être obtenu simplement avec if, mais il existe des cas où continue sera plus joli.
Quand il y a une boucle à l'intérieur d'une autre boucle, un break ou un continue n'affectera que la boucle interne. Parfois, vous aurez envie de sauter en dehors de la boucle extérieure. Pour être capable de référencer une boucle spécifique, les boucles peuvent être labellisées. Un label est un nom (n'importe quel nom de variable fera l'affaire), suivi d'un deux-points (:).
exterieur: for (var coteA = 1; coteA < 10; coteA++) {
interieur: for (var coteB = 1; coteB < 10; coteB++) {
var hypotenuse = Math.sqrt(coteA * coteA + coteB * coteB);
if (hypotenuse % 1 == 0) {
print("Un triangle rectangle avec ses côtés adjacents à l'angle droit de longueurs ",
coteA, " et ", coteB, " a une hypoténuse de ",
hypotenuse, ".");
break exterieur;
}
}
}Ensuite, il existe une construction appelée switch qui peut être utilisée pour choisir quel code exécuter suivant une certaine valeur. C'est quelque chose d'utile, mais la syntaxe JavaScript utilisée pour cela (qui est empruntée au langage de programmation C) est si bizarre et moche que je préfère en général utiliser une chaîne de if à la place.
function conseilMeteo(meteo) {
switch(meteo) {
case "pluvieux":
print("Pensez à prendre un parapluie.");
break;
case "ensoleillé":
print("Habillez-vous légèrement.");
case "nuageux":
print("Allez dehors.");
break;
default:
print("Type de temps inconnu : ", meteo);
break;
}
}
conseilMeteo("ensoleillé");À l'intérieur du bloc ouvert par switch, vous pouvez écrire un certain nombre de labels case. Le programme sautera au label qui correspond à la valeur donnée au switch, ou sautera à default si on ne trouve aucune valeur correspondante. Il commence alors à exécuter les instructions à cet endroit, et continue à travers les autres labels, jusqu'à ce qu'il atteigne un break. Dans certains cas, comme le cas "ensoleillé" dans notre exemple, cela permet de partager du code entre plusieurs cas (il est recommandé d'aller dehors à la fois pour le temps ensoleillé et pour le temps nuageux). La plupart du temps, cela ajoute juste beaucoup de break pas très jolis, ou bien cause des problèmes quand vous oubliez d'en ajouter un.
Comme pour les boucles, on peut donner un label aux structures switch.
Enfin, il y a le mot-clé nommé with. Je ne l'ai en fait jamais utilisé dans un programme réel, mais j'ai vu d'autres personnes l'utiliser, il peut donc être utile de savoir ce que c'est. Le code utilisant with ressemble à ceci :
var pointDeVue = "extérieur";
var objet = {nom: "Ignatius", pointDeVue: "intérieur"};
with(objet) {
print("Nom == ", nom, ", point de vue == ", pointDeVue);
nom = "Raoul";
var nouvelleVariable = 49;
}
show(objet.nom);
show(nouvelleVariable);À l'intérieur du bloc, les propriétés de l'objet passé à with agissent comme des variables. Des variables nouvellement introduites ne sont toutefois pas ajoutées à l'objet. Je suppose que l'idée derrière cette construction était que cela pouvait être utile dans des méthodes qui utilisent beaucoup les propriétés de leur objet. Vous pouvez commencer de telles méthodes avec with(this) {...}, et ainsi ne pas avoir à écrire this tout le temps après cela.
XVI. Tas binaires▲
Dans le , le tas binaire était introduit comme une méthode pour stocker une collection d'objets d'une façon que le plus petit élément soit rapidement trouvé. Comme promis, cet appendice va expliquer les détails derrière cette structure de données.
Étudions de nouveau le problème à résoudre. L'algorithme A* créait une grande quantité de petits objets, et devait les conserver dans une 'liste ouverte'. Il supprimait également constamment les plus petits objets de la liste. L'approche la plus simple aurait été de conserver simplement les objets dans un tableau, et de chercher le plus petit élément que l'on pouvait trouver quand nous en avions besoin. Mais, à moins que nous ayons beaucoup de temps, ça ne fonctionnera pas. Trouver le plus petit élément dans un tableau non trié nécessite de parcourir tout le tableau et de vérifier chaque élément.
La solution suivante aurait été, bien entendu, de trier notre tableau. Les tableaux JavaScript ont une magnifique méthode sort, qui peut être utilisée pour des tâches difficiles. Malheureusement, retrier un tableau entier chaque fois qu'un élément est supprimé demande plus de travail que chercher simplement la valeur minimale dans un tableau non trié. On peut utiliser certaines astuces, par exemple, au lieu de retrier tout le tableau, s'assurer simplement que les nouvelles valeurs sont insérées au bon endroit, ce qui permet au tableau, qui était trié auparavant, de rester trié. Cela se rapproche de la méthode que le tas binaire utilise déjà, mais insérer une valeur au milieu d'un tableau nécessite de déplacer tous les éléments après lui d'une case, ce qui est encore trop lent.
Une autre approche est de ne pas utiliser de tableau du tout, mais de stocker les valeurs dans un ensemble d'objets interconnectés. Un exemple simple de cela est que chaque objet contienne un ou deux (ou moins) liens vers d'autres objets. Il y a un objet racine, contenant la valeur la plus petite, qui est utilisée pour accéder à tous les autres objets. Les liens pointent toujours vers des objets ayant des valeurs plus grandes, la structure globale ressemble donc à quelque chose comme ça :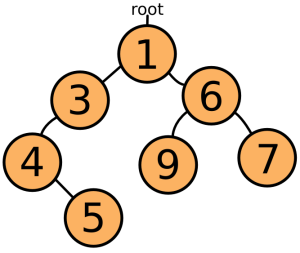
De telles structures sont appelées des arbres, à cause de la façon dont elles se séparent en branches. Maintenant, lorsque vous cherchez le plus petit élément, vous avez juste à prendre l'élément supérieur et réarranger l'arbre pour que l'un des fils de cet élément supérieur - celui avec la plus petite valeur - devienne le nouvel élément supérieur. Lorsque vous insérez de nouveaux éléments, vous 'descendez' l'arbre jusqu'à ce que vous trouviez un élément plus petit que ce nouvel élément, et vous l'insérez à cet endroit. Cela nécessite beaucoup moins de recherches que dans un tableau trié, mais cela a l'inconvénient de créer beaucoup d'objets, ce qui ralentit aussi les choses.
Un tas binaire, lui, utilise un tableau trié, mais il n'est que partiellement trié, un peu comme l'arbre ci-dessus. Au lieu d'objets, les positions dans le tableau sont utilisées pour former l'arbre, comme ce qu'essaie de montrer cette image :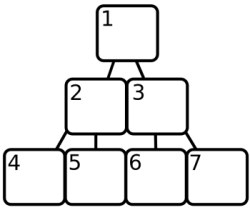
L'élément 1 du tableau est la racine de l'arbre, les éléments 2 et 3 sont ses fils, et d'une façon générale, l'élément X du tableau a comme fils les éléments X * 2 et X * 2 + 1. Vous pouvez voir pourquoi cette structure est appelée 'tas' . Remarquez que ce tableau commence à 1 alors que les tableaux JavaScript commencent à 0. Le tas conserve toujours son plus petit élément en 1, et s'assure que pour tout élément du tableau à la position X, l'élément X/2 (arrondi à l'inférieur) est plus petit.
Pour trouver désormais le plus petit élément, il faut prendre l'élément à la position 1. Mais quand cet élément est supprimé, le tas doit s'assurer qu'il ne reste pas de trous dans le tableau. Pour cela, il prend le dernier élément du tableau, et le remonte au départ. Il le compare ensuite avec ses éléments fils aux positions 2 et 3. Il est probable qu'ils seront plus grands, on l'échange donc avec l'un d'entre eux, et le processus de comparaison avec ses fils est répété pour la nouvelle position, et ainsi de suite, jusqu'à arriver à une position où ses fils sont plus grands, ou à une position où il n'a pas de fils.
[2, 3, 5, 4, 8, 7, 6]
On enlève 2, on déplace 6 au début.
[6, 3, 5, 4, 8, 7]
6 est plus grand que son premier fils 3, donc on les échange.
[3, 6, 5, 4, 8, 7]
Maintenant 6 a pour fils 4 et 8 (position 4 et 5). Il est plus grand que
4, donc on les échange de nouveau.
[3, 4, 5, 6, 8, 7]
6 est en position 4, et n'a plus de fils. Le tas est de nouveau trié.De la même façon, lorsqu'un élément est ajouté au tas, on le met à la fin du tableau et on l'autorise à 'remonter' (comme une bulle de savon) en l'échangeant de façon répétée avec son parent, jusqu'à ce que l'on trouve un parent qui est plus petit que le nouvel élément.
[3, 4, 5, 6, 8, 7]
On joute l'élément 2 de nouveau, il démarre à la fin.
[3, 4, 5, 6, 8, 7, 2]
2 est en position 7, son parent est en position 3, où se trouve un 5.
5 est plus grand que 2, donc on les échange.
[3, 4, 2, 6, 8, 7, 5]
Le parent de la position 3 est la position 1. De nouveau, on échange.
[2, 4, 3, 6, 8, 7, 5]
L'élément ne peut pas aller plus loin que la position 1, on a donc fini.Remarquez comment l'ajout et la suppression d'un élément ne nécessitent plus de le comparer à tous les éléments du tableau. En fait, comme les sauts entre parents et enfants deviennent de plus en plus grands à mesure que le tableau grandit, cet avantage est particulièrement important lorsque vous avez de nombreux éléments.(24)
Voici le code complet de l'implémentation du tas binaire. Deux choses sont à noter. Premièrement, au lieu de comparer directement les éléments mis dans le tas, une fonction (fonctionScore) est appliquée en premier lieu, ce qui permet de stocker des éléments qui ne peuvent pas être comparés directement.
Deuxièmement, comme les tableaux JavaScript commencent en 0, et que les calculs parents/fils utilisent un système qui démarre en 1, il y a quelques calculs bizarres pour compenser cette différence.
function BinaryHeap(fonctionScore){
this.contenu = [];
this.fonctionScore = fonctionScore;
}
BinaryHeap.prototype = {
push: function(element) {
// Ajouter le nouvel élément à la fin du tableau.
this.contenu.push(element);
// L'autoriser à remonter.
this.bubbleUp(this.contenu.length - 1);
},
pop: function() {
// Stocker le premier élément, pour pouvoir le renvoyer plus tard
var resultat = this.contenu[0];
// Récupérer l'élément à la fin du tableau.
var fin = this.contenu.pop();
// S'il reste au moins un élément,
// mettre le dernier élément au début et le faire descendre
if (this.contenu.length > 0) {
this.contenu[0] = fin;
this.sinkDown(0);
}
return resultat;
},
remove: function(noeud) {
var longueur = this.contenu.length;
// Pour supprimer une valeur,
// nous devons parcourir le tableau pour la trouver
for (var i = 0; i < longueur; i++) {
if (this.contenu[i] == noeud) {
// Comme on l'a trouvé, on répète le processus vu dans 'pop'
// pour boucher le trou
var end = this.contenu.pop();
if (i != longueur - 1) {
this.contenu[i] = end;
if (this.fonctionScore(end) < this.fonctionScore(noeud))
this.bubbleUp(i);
else
this.sinkDown(i);
}
return;
}
}
throw new Error("Noeud non trouvé.");
},
size: function() {
return this.contenu.length;
},
bubbleUp: function(n) {
// On va chercher l'élément qui doit être déplacé
var element = this.contenu[n];
// Quand il est à 0, un élément ne peut pas remonter plus haut
while (n > 0) {
// Calculer l'index du parent de l'élément, et aller le chercher.
var parentN = Math.floor((n + 1) / 2) - 1,
parent = this.contenu[parentN];
// Echanger les éléments si le parent est plus grand.
if (this.fonctionScore(element) < this.fonctionScore(parent)) {
this.contenu[parentN] = element;
this.contenu[n] = parent;
// Mettre à jour 'n' pour continuer à la nouvelle position.
n = parentN;
}
// On a trouvé un parent qui est plus petit,
// ce n'est pas nécessaire de le faire bouger davantage.
else {
break;
}
}
},
sinkDown: function(n) {
// Récupérer l'élément cible et son score.
var longueur = this.contenu.length,
element = this.contenu[n],
scoreElement = this.fonctionScore(element);
while(true) {
// Calculer les indices des éléments fils.
var fils2N = (n + 1) * 2, fils1N = fils2N - 1;
// On utilise cela pour stocker la nouvelle position de l'élément,
// s'il y en a une.
var aEchanger = null;
// Si le premier fils existe (est à l'intérieur du tableau)...
if (fils1N < longueur) {
// On le récupère et on calcule son score.
var fils1 = this.contenu[fils1N],
scoreFils1 = this.fonctionScore(fils1);
// Si le score est plus petit que celui de notre élément, on doit échanger
if (scoreFils1 < scoreElement)
aEchanger = fils1N;
}
// Faire les mêmes vérifications pour l'autre fils.
if (fils2N < longueur) {
var fils2 = this.contenu[fils2N],
scoreFils2 = this.fonctionScore(fils2);
if (scoreFils2 < (aEchanger == null ? scoreElement : scoreFils1))
aEchanger = fils2N;
}
// Si l'élément doit être déplacé, on échange et on continue.
if (aEchanger != null) {
this.contenu[n] = this.contenu[aEchanger];
this.contenu[aEchanger] = element;
n = aEchanger;
}
// Sinon, on a fini.
else {
break;
}
}
}
};Et un test simple...



